Construire des polyèdres en bois donc d'une certaine épaisseur
Page 1 sur 1
 Construire des polyèdres en bois donc d'une certaine épaisseur
Construire des polyèdres en bois donc d'une certaine épaisseur

1/2 octaèdre régulier
Si on veut construire des polyèdres en bois il faut régler l'angle de coupe avec la scie radiale pour créer la bonne inclinaison.
Et pour cela il faut faire un peu de géométrie.
- tétraèdre régulier : 4 triangles équilatéraux
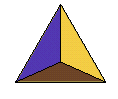
- cube ou hexaèdre : 6 carrés

- octaèdre régulier : 8 triangles équilatéraux
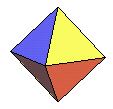
- dodécaèdre (régulier) : 12 pentagones réguliers
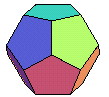
- icosaèdre (régulier) : 20 triangles équilatéraux
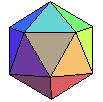
Voir site : https://www.mathcurve.com/polyedres/regulier/regulier.shtml
d'après ce site l'angle dièdre vaut :

Mais comment trouver l'angle soi-même...
Et puis l'angle du dièdre n'est pas l'angle de coupe!
l'angle de coupe est le complément à 90° de la moitié de l'angle dièdre
_________________________________________________________________________________________
tétraèdre régulier

On cherche donc l'angle du dièdre au sommet d'un triangle isocèle de côté 0.866a et la base vaut a
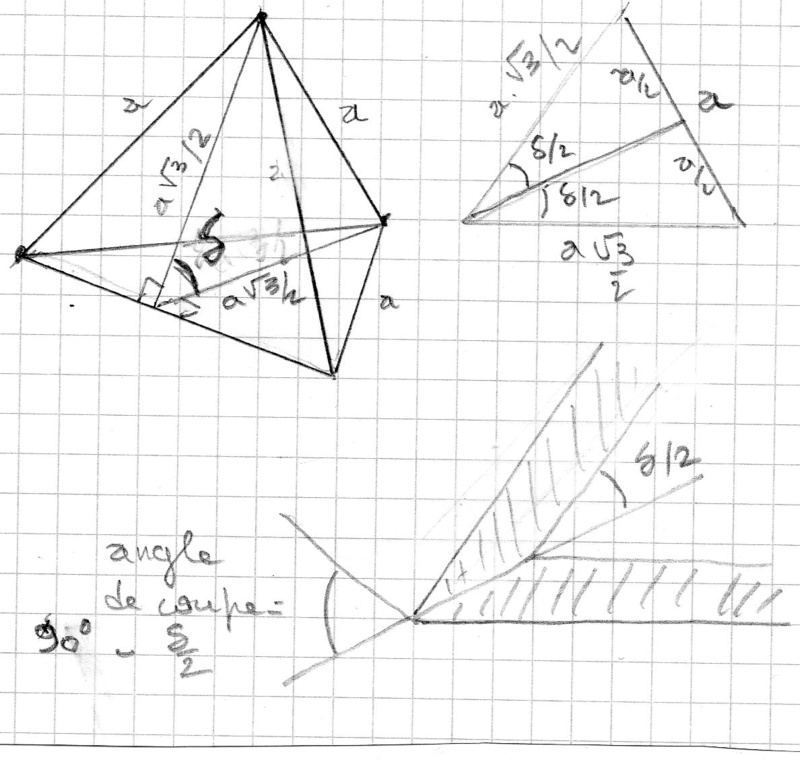
la moitié de cet angle dièdre est l'angle d'un triangle rectangle de côté a/2
le sinus de la moitié de cet angle dièdre vaut donc (a/2)/(a*racine(3)/2) c'est à dire 1/racine(3)
donc la moitié de cet angle dièdre vaut arcsin(1/racine(3)) soit 35°264
Angle de coupe du tétraèdre régulier = 54°736
(Mais c'est impossible à couper car une scie radiale ne s'incline que de 45° au plus!...
______________________________________________________________________________
Cube ou Hexaèdre

angle de coupe du cube : 45°
C'est donc possible de le couper à la scie radiale.
______________________________________________________________________________
octaèdre régulier


donc la moitié de cet angle dièdre vaut arccos(1/racine(3)) soit 54°736
Angle de coupe de l'octaèdre régulier = 35°264
Encore plus facile à couper avec la scie radiale
______________________________________________________________________________
dodécaèdre (régulier)

Alors il faut regarder le pentagone
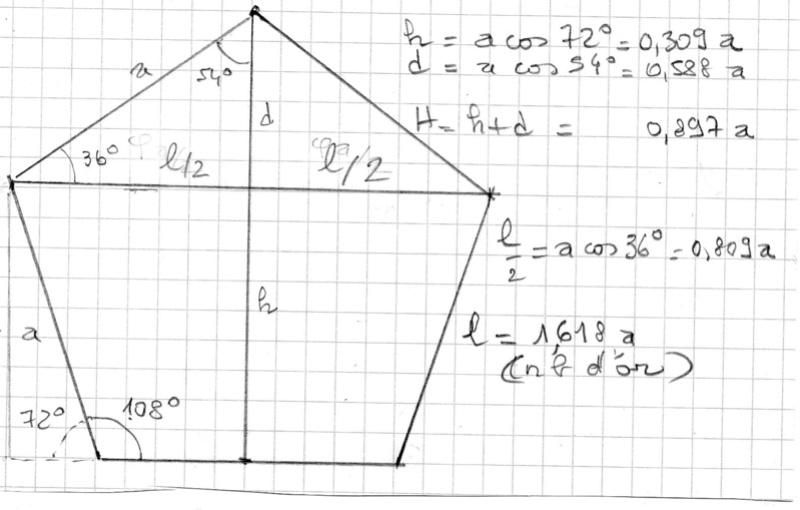
et ensuite quand on assemble 4 pentagones on fabrique une sorte de carré de côté 1.618a (nombre d'or)
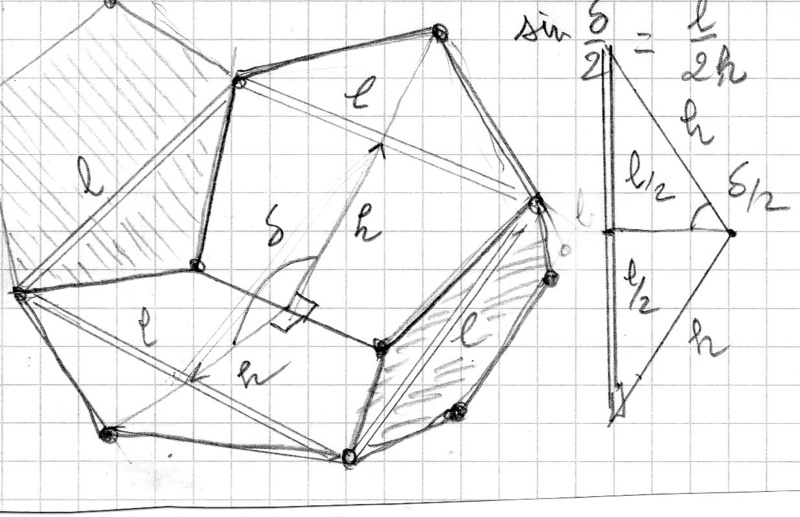
donc le demi-dièdre vaut 58°,29 (nota pour vérifier wiki dit que le dièdre vaut 116°33'54")
l'angle de coupe du dodécaèdre régulier vaut 31°714
________________________________________________________________________________
isocaèdre (régulier)

l'assemblage de 5 triangles forme un pentagone

le demi-dièdre vaut 69°09
l'angle de coupe de l'isocaèdre régulier vaut 20°93 soit presque 21°
et si on coupe un peu plus les côtés seront jointifs devant et laisseront de la place pour la colle derrière...
_________________________________________________________________________________
Mais pourquoi tous ces calculs? Parce que je veux construire un icosidodécaèdre
icosidodécaèdre : 12 pentagones et 20 triangles
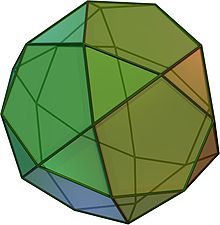
https://fr.wikipedia.org/wiki/Icosidod%C3%A9ca%C3%A8dre
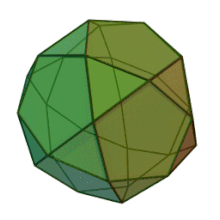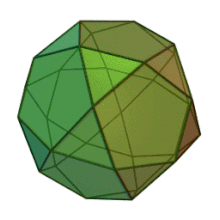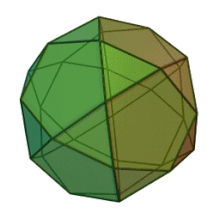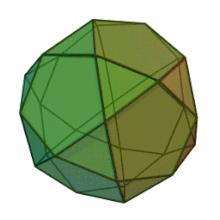
Et là il faut un angle de coupe pour le triangle et un pour le pentagone

On ne peut pas diviser l'angle du dièdre en deux pour trouver le complément de l'angle de coupe!

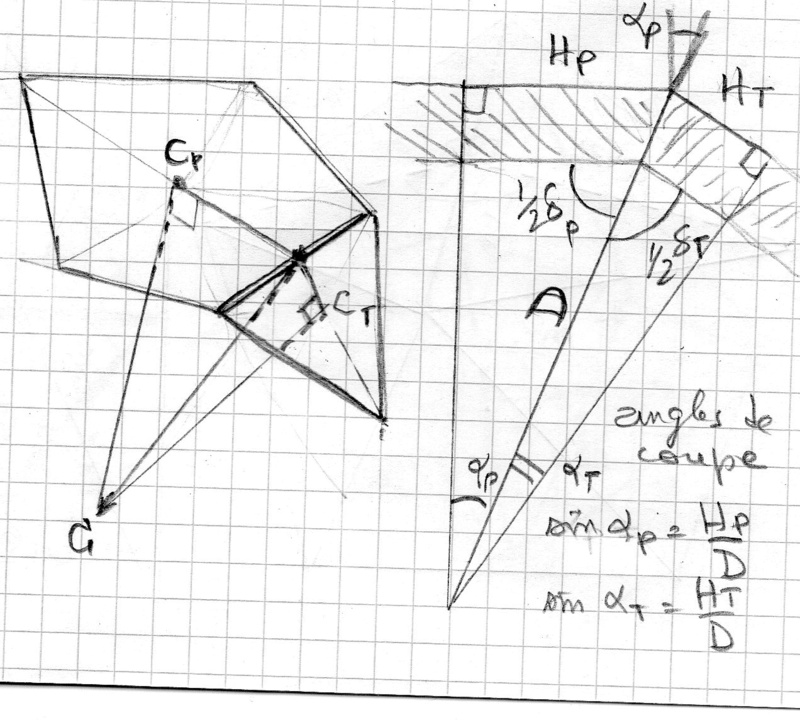
A cause de la symétrie le centre du pentagone et le centre du triangle équilatéral visent le centre avec un angle droit.
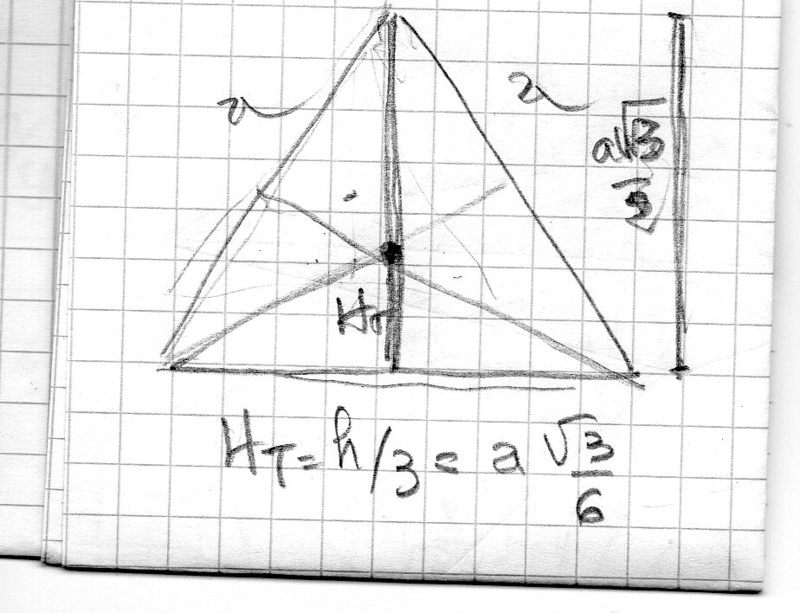
la hauteur du centre du triangle est simple :
Quant à celle du pentagone c'est un peu plus compliqué :

Le sinus des angles de coupe = H /D
Pentagone : le sinus vaut 0.688a/1.539a = 0.447
l'angle de coupe du pentagone de l'icosidodécaèdre vaut 26°554 soit presque 27°
Triangle équilatéral : le sinus vaut 0.288a/1.539a = 0.187
l'angle de coupe du triangle de l'icosidodécaèdre vaut 10°785 soit presque 11°

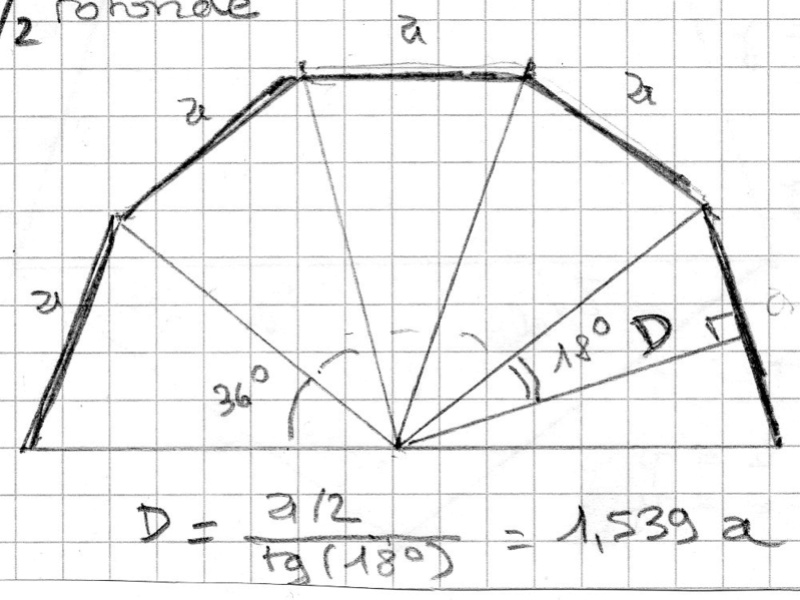
Ensuite pour savoir dans quelles planches tailler les pentagones il faut connaitre la hauteur du pentagone 1,539 a
à comparer avec la hauteur du triangle équilatéral 0,866a
Avec les chutes des placards de soupente : https://jardindesprit.forumgratuit.org/t1680-habillage-de-soupente-avec-des-placards-sur-mesure
j'ai réalisé un cube et un demi-octaèdre et un demi-icosidodécaèdre
et avec quelques chutes de découpe de la terrasse : https://jardindesprit.forumgratuit.org/t1688-la-nouvelle-baie-vitree-nous-impose-de-creer-une-terrasse-en-bois-composite
j'ai fait un peu d'architecture...


Mais même en faisant très attention avec la scie radiale on coupe à 1 mm près et cela ne suffit pas pour ajuster correctement tous les morceaux...
On peut aussi aller consulter le site : http://www.mathcurve.com/polyedres/icosidodecaedre/icosidodecaedre.shtml
mais il ne donne pas les angles de coupe!
Il fournit de très belles photos :

http://www.mathcurve.com/polyedres/icosidodecaedre/icosidodecaedre.shtml
Ballon à tressage icosidodécaèdrique servant dans un jeu traditionnel aux Philippines
Dernière édition par Ulysse92 le Mar 2 Jan 2018 - 12:11, édité 1 fois
 Re: Construire des polyèdres en bois donc d'une certaine épaisseur
Re: Construire des polyèdres en bois donc d'une certaine épaisseur
Je ne suis pas le seul à aimer les polyèdres...
Il y a un très beau blog sur le polyèdre dans la peinture : http://enigm-art.blogspot.fr/2012/11/le-polyedre-dans-la-peinture.html
Léonard de Vinci

http://enigm-art.blogspot.fr/2012/11/le-polyedre-dans-la-peinture.html
http://compagnonnage.info/blog/blogs/blog1.php/2008/05/01/l-ascension-des-polyedres-en-pierre
Et un autre : http://compagnonnage.info/blog/blogs/blog1.php/2008/05/01/l-ascension-des-polyedres-en-pierre

http://compagnonnage.info/blog/blogs/blog1.php/2008/05/01/l-ascension-des-polyedres-en-pierre
Luca Pacioli faisant la démonstration d'un théorème d'Euclide (tableau de 1495 attribué à Jacopo de Barbari).

http://compagnonnage.info/blog/blogs/blog1.php/2008/05/01/l-ascension-des-polyedres-en-pierre
Mosaïque de marbre par Paolo Uccello (1397-1475) à la basilique Saint-Marc de Venise
Et puis encore :

https://puzzles-et-casse-tete.blog4ever.com/pocoloco
un casse-tête avec le plan de construction

http://www.kad-gallery.com/awalter_2.html
Antoine W A L T E R

http://www.acbx41.com/article-35116283.html
'Le Bois, du coeur à l'ouvrage' au palais de la Découverte

http://jeanmichelunger.free.fr/polyedres.html
Jean Michel Unger sculpteur

ttp://jeanmichelunger.free.fr/polyedres.html
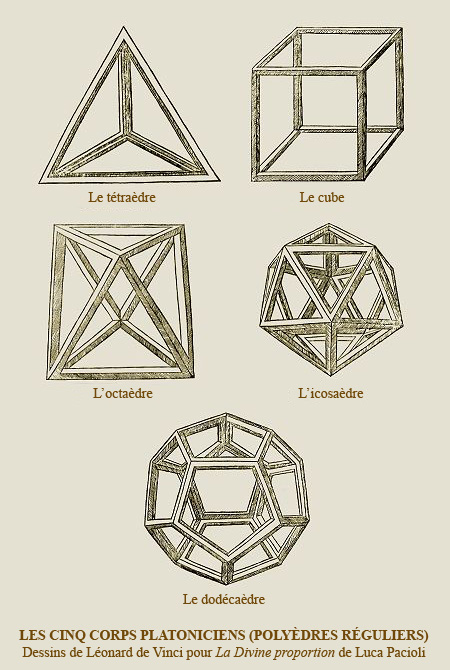
Les cinq corps de Platon :

https://www.mathsisfun.com/geometry/polyhedra-images.html
Gravure d'Augustin Herschvogel (1503-1553)

https://www.mathcurve.com/polyedres/icosaedre/icosaedre.shtml
Icosaèdre à la "Léonard de Vinci" réalisé par Patrice Gaumeton, ébéniste à Paris.

https://www.etsy.com/fr/listing/227436765/10-perles-geometriques-en-bois-marron-20

http://maths.ac-noumea.nc/polyhedr/stuff/AMC/AMC_troph.htm

http://www.apprendre-en-ligne.net/blog/index.php/?q=poly%C3%A8dres
http://www.ict.griffith.edu.au/anthony/graphics/polyhedra/

hhttp://lesateliersdelavesnois.fr/ateliers_artistes_avesnois_gagneux.htm
Roland Gagneux ; Pentaki dodécaèdre adouci 140 faces triangle

http://www.imgrum.org/media/1404515810453991226_299650645
Octaèdre étoilé : tombe d'André Breton

https://deavita.fr/design-interieur/idees-amenagement-interieur-bois/
table basse polyèdre en bois massif

http://habitat-bulles.com/sebastien-baldini/



http://www.plumetismagazine.net/decoration-polyedres/
Table ou tabouret Icosaèdre

http://compagnonnage.info/blog/blogs/blog1.php/2009/10/25/polyedre-pas-a-pas
Taille pas à pas d'un polyèdre en bois massif
Il y a un très beau blog sur le polyèdre dans la peinture : http://enigm-art.blogspot.fr/2012/11/le-polyedre-dans-la-peinture.html
Léonard de Vinci

http://enigm-art.blogspot.fr/2012/11/le-polyedre-dans-la-peinture.html

http://compagnonnage.info/blog/blogs/blog1.php/2008/05/01/l-ascension-des-polyedres-en-pierre
Et un autre : http://compagnonnage.info/blog/blogs/blog1.php/2008/05/01/l-ascension-des-polyedres-en-pierre

http://compagnonnage.info/blog/blogs/blog1.php/2008/05/01/l-ascension-des-polyedres-en-pierre
Luca Pacioli faisant la démonstration d'un théorème d'Euclide (tableau de 1495 attribué à Jacopo de Barbari).

http://compagnonnage.info/blog/blogs/blog1.php/2008/05/01/l-ascension-des-polyedres-en-pierre
Mosaïque de marbre par Paolo Uccello (1397-1475) à la basilique Saint-Marc de Venise
Et puis encore :

https://puzzles-et-casse-tete.blog4ever.com/pocoloco
un casse-tête avec le plan de construction


http://www.kad-gallery.com/awalter_2.html
Antoine W A L T E R

http://www.acbx41.com/article-35116283.html
'Le Bois, du coeur à l'ouvrage' au palais de la Découverte

http://jeanmichelunger.free.fr/polyedres.html
Jean Michel Unger sculpteur

ttp://jeanmichelunger.free.fr/polyedres.html
Les cinq corps de Platon :

https://www.mathsisfun.com/geometry/polyhedra-images.html
Gravure d'Augustin Herschvogel (1503-1553)

https://www.mathcurve.com/polyedres/icosaedre/icosaedre.shtml
Icosaèdre à la "Léonard de Vinci" réalisé par Patrice Gaumeton, ébéniste à Paris.

https://www.etsy.com/fr/listing/227436765/10-perles-geometriques-en-bois-marron-20

http://maths.ac-noumea.nc/polyhedr/stuff/AMC/AMC_troph.htm


http://www.apprendre-en-ligne.net/blog/index.php/?q=poly%C3%A8dres
http://www.ict.griffith.edu.au/anthony/graphics/polyhedra/

hhttp://lesateliersdelavesnois.fr/ateliers_artistes_avesnois_gagneux.htm
Roland Gagneux ; Pentaki dodécaèdre adouci 140 faces triangle

http://www.imgrum.org/media/1404515810453991226_299650645
Octaèdre étoilé : tombe d'André Breton

https://deavita.fr/design-interieur/idees-amenagement-interieur-bois/
table basse polyèdre en bois massif

http://habitat-bulles.com/sebastien-baldini/



http://www.plumetismagazine.net/decoration-polyedres/
Table ou tabouret Icosaèdre

http://compagnonnage.info/blog/blogs/blog1.php/2009/10/25/polyedre-pas-a-pas
Taille pas à pas d'un polyèdre en bois massif
 Et si on les créait en virtuel...
Et si on les créait en virtuel...
Voilà des créations étonnantes de TaffGoch:
Suivez les liens pour avoir plus d'explications

https://taffgoch.deviantart.com/art/Rotegrity-Woodwork-201870495
Ce n'est qu'un dessin virtuel... mais habilement traité pour donner plus de profondeur!

https://taffgoch.deviantart.com/art/Rotegrity-1v-0-1-625449702

Cela coûterait cher à réaliser en impression 3D.
animation flash : https://taffgoch.deviantart.com/art/62-Gears-Render-Flash-Anim-252683466
TaffGoch dit qu'il a été inspiré par bugman : https://bugman123.deviantart.com/art/242-Gear-Sphere-261164254

https://bugman123.deviantart.com/art/Geodesic-Dome-Gear-204949245
Suivez les liens pour avoir plus d'explications

https://taffgoch.deviantart.com/art/Rotegrity-Woodwork-201870495
Ce n'est qu'un dessin virtuel... mais habilement traité pour donner plus de profondeur!

https://taffgoch.deviantart.com/art/Rotegrity-1v-0-1-625449702

Cela coûterait cher à réaliser en impression 3D.
animation flash : https://taffgoch.deviantart.com/art/62-Gears-Render-Flash-Anim-252683466
TaffGoch dit qu'il a été inspiré par bugman : https://bugman123.deviantart.com/art/242-Gear-Sphere-261164254

https://bugman123.deviantart.com/art/Geodesic-Dome-Gear-204949245
 Sujets similaires
Sujets similaires» Whisky tourbé? un nouvel émoi
» Ulysse92 - peintures et sculptures
» La nouvelle baie vitrée nous impose de créer une terrasse (en bois composite)
» Gehard Demetz - sculptures sur bois
» Fondation Louis Vuitton au Bois de Boulogne
» Ulysse92 - peintures et sculptures
» La nouvelle baie vitrée nous impose de créer une terrasse (en bois composite)
» Gehard Demetz - sculptures sur bois
» Fondation Louis Vuitton au Bois de Boulogne
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum|
|
|





