art et mathématique, Pierre Gallais
jardin d'esprit :: Archives :: Sublimation des arts plastiques :: Les créations récentes de nouveaux artistes
Page 1 sur 1
 art et mathématique, Pierre Gallais
art et mathématique, Pierre Gallais
Conférence donnée par Pierre Galais le samedi 3 septembre à 18h au GAC d'Annonay (Groupement d'Art Contemporain)

http://www.gac-annonay.org/GAC/Groupe_dArt_Contemporain.html
NdlR :L'harmattan est un vent de l'Afrique de l'Ouest et un éditeur qui a pour but de publier des ouvrages traitant des problèmes du Tiers-Monde et de l’Afrique
ici c'est juste un jeu de mots

https://www.makemevip.info/actualites/autre/pierre-gallais-artiste-et-mathematicien
Pierre Gallais
son site est là : http://www.institutdemathologie.fr/
ses installations :

https://www.artactif.com/centredart/galerie/index17546.htm#.V8rPPq08DYg
intersections

http://www.institutdemathologie.fr/urban-art-installations-in-situ/au-lycee/item/au-lycee.html?category_id=22
Pythagore

http://idm-old.math.cnrs.fr/Ma-thematique-en-situation.html
MATHou
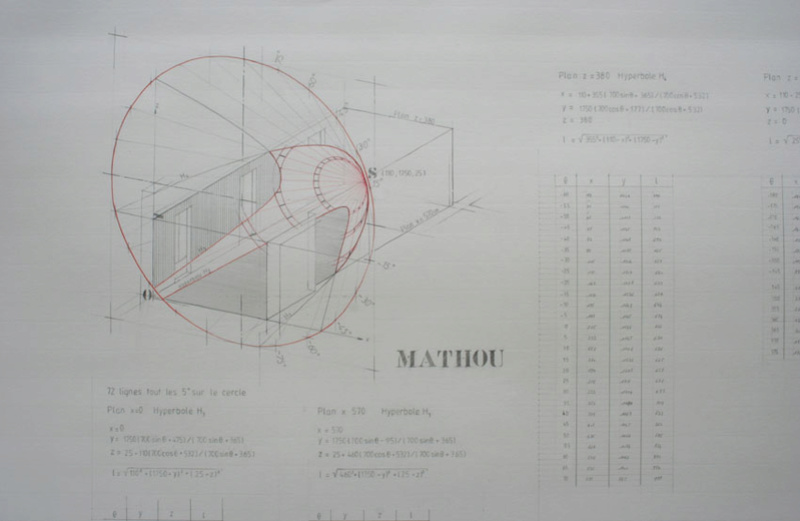
un peu comme Christo, les plans préparatifs de ses installations sont très beaux, dessinés au crayon graphite voire peint avec le pinceau le plus fin


http://images.math.cnrs.fr/Cubage.html
cubage

http://images.math.cnrs.fr/Cubage.html

http://images.math.cnrs.fr/Cubage.html
Anamorphoses : SéMATHphore

au mauvais endroit

http://images.math.cnrs.fr/SeMATHphore.html
au bon endroit
le rond rouge qui n'est pas en anamorphose pousse notre cerveau à faire flotter le X
Etudes des ellipses (la boîte à Pilchard du vendredi de son enfance) et ellipsoïdes

http://images.math.cnrs.fr/Pierre-Gallais-artiste-et.html
une sphère virtuelle se transforme en ellipsoïde virtuel en l'applatissant un peu
figure tirée du livre de Hilbert et Cohn-Vossen

http://images.math.cnrs.fr/Pierre-Gallais-artiste-et.html
le site Paillart

http://idm-old.math.cnrs.fr/Un-site-paillart.html

Intersections du tore : projet pour les marches du palais de justice d’Aix-en-Provence

http://images.math.cnrs.fr/Lorsque-les-tores-sont-partages.html
Lorsque les tores sont partagés

Lundi 5 septembre :
Reste un point cependant...
Avec les outils mathématiques d'aujourd'hui disponibles sur ordinateur il n'y a plus toute cette transpiration...
alors Pierre Gallais va devoir investir autre chose! Et plus laisser cours à son imagination.
Et puis son art est quelquefois une sorte de manièrisme. On essaye d'esbrouffer le visiteur par cette maîtrise des intersections. Dans l'histoire de l'art il a fallu Le Caravage pour faire cesser toutes ces peintures en contreplonglée à la Dali et on est passé au pouvoir de la lumière, du clair obscur.
Heureusement il a de la ressource et ses jeux de bottes nous poussaient plutôt vers une rêverie à la Christo avec en tête Stonehenge que vers l'adoration des ellipses.

http://images.math.cnrs.fr/Ceci-n-est-pas-une-mise-en-boite.html
ceci n'est pas une mise en boîte

http://images.math.cnrs.fr/Les-ficelles-du-Pilchart.html?id_forum=7062
Les ficelles du Pilchart (pour la fête des lumières à Lyon)

http://images.math.cnrs.fr/Un-petit-bijou.html
un petit bijou

http://images.math.cnrs.fr/Un-petit-bijou.html

http://www.gac-annonay.org/GAC/Groupe_dArt_Contemporain.html
NdlR :L'harmattan est un vent de l'Afrique de l'Ouest et un éditeur qui a pour but de publier des ouvrages traitant des problèmes du Tiers-Monde et de l’Afrique
ici c'est juste un jeu de mots

https://www.makemevip.info/actualites/autre/pierre-gallais-artiste-et-mathematicien
Pierre Gallais
son site est là : http://www.institutdemathologie.fr/
ses installations :

https://www.artactif.com/centredart/galerie/index17546.htm#.V8rPPq08DYg
intersections

http://www.institutdemathologie.fr/urban-art-installations-in-situ/au-lycee/item/au-lycee.html?category_id=22
Pythagore

http://idm-old.math.cnrs.fr/Ma-thematique-en-situation.html
MATHou

un peu comme Christo, les plans préparatifs de ses installations sont très beaux, dessinés au crayon graphite voire peint avec le pinceau le plus fin


http://images.math.cnrs.fr/Cubage.html
cubage

http://images.math.cnrs.fr/Cubage.html

http://images.math.cnrs.fr/Cubage.html
Anamorphoses : SéMATHphore

au mauvais endroit

http://images.math.cnrs.fr/SeMATHphore.html
au bon endroit
le rond rouge qui n'est pas en anamorphose pousse notre cerveau à faire flotter le X
Etudes des ellipses (la boîte à Pilchard du vendredi de son enfance) et ellipsoïdes

http://images.math.cnrs.fr/Pierre-Gallais-artiste-et.html
une sphère virtuelle se transforme en ellipsoïde virtuel en l'applatissant un peu
figure tirée du livre de Hilbert et Cohn-Vossen

http://images.math.cnrs.fr/Pierre-Gallais-artiste-et.html
le site Paillart

http://idm-old.math.cnrs.fr/Un-site-paillart.html

Intersections du tore : projet pour les marches du palais de justice d’Aix-en-Provence

http://images.math.cnrs.fr/Lorsque-les-tores-sont-partages.html
Lorsque les tores sont partagés

Lundi 5 septembre :
Reste un point cependant...
Avec les outils mathématiques d'aujourd'hui disponibles sur ordinateur il n'y a plus toute cette transpiration...
alors Pierre Gallais va devoir investir autre chose! Et plus laisser cours à son imagination.
Et puis son art est quelquefois une sorte de manièrisme. On essaye d'esbrouffer le visiteur par cette maîtrise des intersections. Dans l'histoire de l'art il a fallu Le Caravage pour faire cesser toutes ces peintures en contreplonglée à la Dali et on est passé au pouvoir de la lumière, du clair obscur.
Heureusement il a de la ressource et ses jeux de bottes nous poussaient plutôt vers une rêverie à la Christo avec en tête Stonehenge que vers l'adoration des ellipses.

http://images.math.cnrs.fr/Ceci-n-est-pas-une-mise-en-boite.html
ceci n'est pas une mise en boîte

http://images.math.cnrs.fr/Les-ficelles-du-Pilchart.html?id_forum=7062
Les ficelles du Pilchart (pour la fête des lumières à Lyon)

http://images.math.cnrs.fr/Un-petit-bijou.html
un petit bijou

http://images.math.cnrs.fr/Un-petit-bijou.html
 Re: art et mathématique, Pierre Gallais
Re: art et mathématique, Pierre Gallais
Rien que pour faire cela

http://images.math.cnrs.fr/Pierre-Gallais-artiste-et.html
une sphère virtuelle se transforme en ellipsoïde virtuel en l'aplatissant un peu
figure tirée du livre de Hilbert et Cohn-Vossen
Comment le calculer?
utiliser Open Office Calc
On voit qu'il y a 7 plans dans un quart de sphère. Si c'était symétrique le 4ème plan tomberait sur 45° or ils sont légèrement décalés.
Il faut supposer que l'angle 90° est découpé en 7,5 soit 12° et qu'on part dans un sens avec un plan à 6° (comme cela le symétrique à -6°) donnera bien 12° et au bout de 7 plans on a 6°+ (7-1)x12° = 78° il reste 12° pour atteindre 90° donc 24° d'angle au centre pour le petit cercle (qui ne doit pas être trop petit pour que ça tienne)
Et pour les perpendiculaires on fait la même chose.
Comme mon imprimante utilise des feuilles A4 21x29,7 je choisis un diamètre de 20cm soit un rayon de 10cm
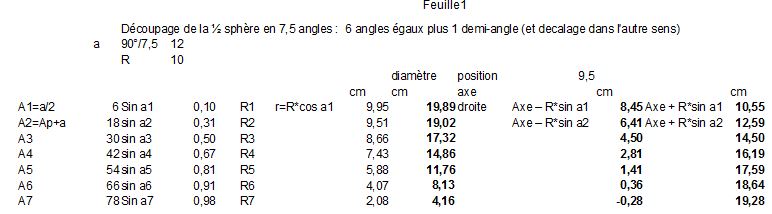
Comment le dessiner?
utiliser Open Office Dessin
Il faut préparer sa feuille de dessin en passant par OUTILS/OPTIONS/open.office.org Draw/général
et y définir l'échelle et l'unité de mesure : choisir centimètres
onglet affichage : activer repères visibles
onglet grille : activer grille visible
Tous les paramètres d'un objet en cours de création, s'affichent en bas de l'écran au dessus de la barre des tâches : longueur - largeur - angle.
Chaque objet est positionnable au millimètre prés avec l'aide du menu contextuel (clic droit) : position et taille.
De plus l'utilisation du zoom ctrl+roulette de souris permet de travailler très finement.
On crée une ellipse pleine, on la vide, on met le diamètre horizontal et vertical et on coche "garder la proportion"
puis on choisit de positionner le centre (cliquer sur le point du menu qui représente le centre) au même endroit 9,5cm pour x et 10cm pour y
On recopie cette ellipse et on change le rayon, etc..
Ensuite on crée une droite verticale qu'on positionne en y=10cm et en x les valeurs calculées dans le tableur. (on peut régler l'épaisseur en fonction du support sur lequel on va imprimer ou transférer le patron)
Quand on a fait le patron du haut on choisit créer diapo et on crée un dessin sur lequel on enlève les cercles intérieurs
et puis on crée une diapo sur laquelle on procède de même

Quand il reste 3 cercles en les déplaçant on peut créer le patron du bas.

Comment l'imprimer?
on imprime chaque feuille en 4 exemplaires
On prépare deux feuilles symétriques avec les fentes vers le bas et on croise en montant deux feuilles symétriques avec les fentes vers le haut
Pas très facile...
on pourrait transférer le patron sur du bristol voire sur du carton ondulé très fin (paquet de gâteau mais il en faut beaucoup) mais quand on découpe il faut tracer des traits plus larges, ce qu'on peut programmer dans le logiciel de dessin) comme cela il seront centrés autour de la bonne cote
On pourrait choisir des vieux CD, régler le calcul avec le rayon qui va bien et l'épaisseur correspondante mais comment découper les Cd : en long avec une scie à métaux
mais en rond??????
On pourrait choisir de très vieux vinyles mais le problème reste le même...
On pourrait le faire en plus petit avec des cageots (bois très fins faciles à couper mais qui se fendent en long...)
On pourrait le feuille avec des feuilles de liège! et un très bon cutter! mais il faut reporter le patron.
On pourrait la faire avec des cartons de chemise colorés qu'on peut même découper pour que ça passe dans l'imprimante
On pourrait imprimer sur chaque face une planisphère vue de l'ouest au recto et au verso vue de l'est
et pour les planches du bas vue du Nord au recto et vue du Sud au verso mais tête en bas car les découpes seront en haut.
Pierre Gallais l'a fait avec un carton ondulé plastifié très fin.

http://images.math.cnrs.fr/Pierre-Gallais-artiste-et.html
une sphère virtuelle se transforme en ellipsoïde virtuel en l'aplatissant un peu
figure tirée du livre de Hilbert et Cohn-Vossen
Comment le calculer?
utiliser Open Office Calc
On voit qu'il y a 7 plans dans un quart de sphère. Si c'était symétrique le 4ème plan tomberait sur 45° or ils sont légèrement décalés.
Il faut supposer que l'angle 90° est découpé en 7,5 soit 12° et qu'on part dans un sens avec un plan à 6° (comme cela le symétrique à -6°) donnera bien 12° et au bout de 7 plans on a 6°+ (7-1)x12° = 78° il reste 12° pour atteindre 90° donc 24° d'angle au centre pour le petit cercle (qui ne doit pas être trop petit pour que ça tienne)
Et pour les perpendiculaires on fait la même chose.
Comme mon imprimante utilise des feuilles A4 21x29,7 je choisis un diamètre de 20cm soit un rayon de 10cm

Comment le dessiner?
utiliser Open Office Dessin
Il faut préparer sa feuille de dessin en passant par OUTILS/OPTIONS/open.office.org Draw/général
et y définir l'échelle et l'unité de mesure : choisir centimètres
onglet affichage : activer repères visibles
onglet grille : activer grille visible
Tous les paramètres d'un objet en cours de création, s'affichent en bas de l'écran au dessus de la barre des tâches : longueur - largeur - angle.
Chaque objet est positionnable au millimètre prés avec l'aide du menu contextuel (clic droit) : position et taille.
De plus l'utilisation du zoom ctrl+roulette de souris permet de travailler très finement.
On crée une ellipse pleine, on la vide, on met le diamètre horizontal et vertical et on coche "garder la proportion"
puis on choisit de positionner le centre (cliquer sur le point du menu qui représente le centre) au même endroit 9,5cm pour x et 10cm pour y
On recopie cette ellipse et on change le rayon, etc..
Ensuite on crée une droite verticale qu'on positionne en y=10cm et en x les valeurs calculées dans le tableur. (on peut régler l'épaisseur en fonction du support sur lequel on va imprimer ou transférer le patron)
Quand on a fait le patron du haut on choisit créer diapo et on crée un dessin sur lequel on enlève les cercles intérieurs
et puis on crée une diapo sur laquelle on procède de même

Quand il reste 3 cercles en les déplaçant on peut créer le patron du bas.

Comment l'imprimer?
on imprime chaque feuille en 4 exemplaires
On prépare deux feuilles symétriques avec les fentes vers le bas et on croise en montant deux feuilles symétriques avec les fentes vers le haut
Pas très facile...
on pourrait transférer le patron sur du bristol voire sur du carton ondulé très fin (paquet de gâteau mais il en faut beaucoup) mais quand on découpe il faut tracer des traits plus larges, ce qu'on peut programmer dans le logiciel de dessin) comme cela il seront centrés autour de la bonne cote
On pourrait choisir des vieux CD, régler le calcul avec le rayon qui va bien et l'épaisseur correspondante mais comment découper les Cd : en long avec une scie à métaux
mais en rond??????
On pourrait choisir de très vieux vinyles mais le problème reste le même...
On pourrait le faire en plus petit avec des cageots (bois très fins faciles à couper mais qui se fendent en long...)
On pourrait le feuille avec des feuilles de liège! et un très bon cutter! mais il faut reporter le patron.
On pourrait la faire avec des cartons de chemise colorés qu'on peut même découper pour que ça passe dans l'imprimante
On pourrait imprimer sur chaque face une planisphère vue de l'ouest au recto et au verso vue de l'est
et pour les planches du bas vue du Nord au recto et vue du Sud au verso mais tête en bas car les découpes seront en haut.
Pierre Gallais l'a fait avec un carton ondulé plastifié très fin.
Dernière édition par Ulysse92 le Lun 5 Sep 2016 - 16:55, édité 7 fois (Raison : ait le faire avec des)
 Sujets similaires
Sujets similaires» Pierre Alechinsky
» Pierre Henry
» Maupassant - Pierre et Jean - lu gratuitement sur mon téléphone
» Le musée d'art naïf de Laval accueille un nouveau Rousseau
» Dimanche 26 février 2012 - Expo "Hey" à la Halle St-Pierre
» Pierre Henry
» Maupassant - Pierre et Jean - lu gratuitement sur mon téléphone
» Le musée d'art naïf de Laval accueille un nouveau Rousseau
» Dimanche 26 février 2012 - Expo "Hey" à la Halle St-Pierre
jardin d'esprit :: Archives :: Sublimation des arts plastiques :: Les créations récentes de nouveaux artistes
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum




